원의 크기와 상관없이 원의 둘레와 지름의 비는 일정한데, 이 비를 원주율이라 하고 @@NAMATH_INLINE@@\pi@@NAMATH_INLINE@@로 나타낸다.

원의 둘레는 내접정다각형의 둘레보다 크고 외접다각형의 둘레보다 작다. 이 사실과 외접원의 반지름의 길이가 @@NAMATH_INLINE@@1@@NAMATH_INLINE@@인 원의 둘레는 @@NAMATH_INLINE@@2\pi@@NAMATH_INLINE@@라는 사실을 이용하면 @@NAMATH_INLINE@@\pi@@NAMATH_INLINE@@의 근삿값을 구할 수 있다.

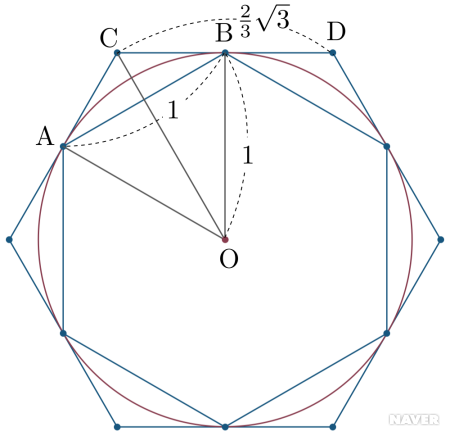
예를 들어, 반지름의 길이가 @@NAMATH_INLINE@@1@@NAMATH_INLINE@@인 원에 내접하는 정육각형의 한 변의 길이는 @@NAMATH_INLINE@@1@@NAMATH_INLINE@@이고 외접하는 정육각형의 한 변의 길이는 @@NAMATH_INLINE@@\frac{2}{3} \sqrt{3}@@NAMATH_INLINE@@이므로 @@NAMATH_INLINE@@6 < 2\pi < 4\sqrt{3}@@NAMATH_INLINE@@임을 알 수 있다. 그러므로 @@NAMATH_DISPLAY@@3 < \pi < 2\sqrt{3}@@NAMATH_DISPLAY@@ 이다. 이로부터 @@NAMATH_INLINE@@\pi@@NAMATH_INLINE@@는 @@NAMATH_INLINE@@3@@NAMATH_INLINE@@보다 크고 @@NAMATH_INLINE@@3.6@@NAMATH_INLINE@@보다는 작음을 알 수 있다. 아래 그림에서 삼각형 @@NAMATH_INLINE@@\text{OAB}@@NAMATH_INLINE@@는 정삼각형이므로 원에 내접하는 정육각형의 한 변의 길이인 @@NAMATH_INLINE@@\overline{\text{AB}}@@NAMATH_INLINE@@의 길이는 @@NAMATH_INLINE@@1@@NAMATH_INLINE@@이고, @@NAMATH_INLINE@@\angle \text{BOC}=30^{\circ}@@NAMATH_INLINE@@이므로 @@NAMATH_INLINE@@\overline{\text{CB}}=\frac{\sqrt{3}}{3}@@NAMATH_INLINE@@이다. 따라서 원에 외접하는 정육각형의 한 변의 길이인 @@NAMATH_INLINE@@\overline{\text{CD}}@@NAMATH_INLINE@@의 길이는 @@NAMATH_INLINE@@\frac{2}{3}\sqrt{3}@@NAMATH_INLINE@@이다.

확대보기

고대 그리스의 수학자 아르키메데스는 이와 같은 방법을 정@@NAMATH_INLINE@@96@@NAMATH_INLINE@@각형까지 적용하였다. 즉, 반지름의 길이 @@NAMATH_INLINE@@1@@NAMATH_INLINE@@인 원에 내접하는 정@@NAMATH_INLINE@@96@@NAMATH_INLINE@@각형의 변의 길이의 합, 외접하는 정@@NAMATH_INLINE@@96@@NAMATH_INLINE@@각형의 변의 길이의 합과 원의 둘레와 비교하여 @@NAMATH_DISPLAY@@3\frac{10}{71} < \pi < 3\frac{1}{7}@@NAMATH_DISPLAY@@임을 보였다. 이를 소수로 나타내면 다음과 같다. @@NAMATH_DISPLAY@@3.14084 < \pi < 3.142858@@NAMATH_DISPLAY@@

반지름의 길이가 @@NAMATH_INLINE@@1@@NAMATH_INLINE@@인 원에 내접하는 @@NAMATH_INLINE@@n@@NAMATH_INLINE@@각형의 넓이와 @@NAMATH_INLINE@@2n@@NAMATH_INLINE@@각형의 넓이를 비교해 보자.

그림에서 원에 내접하는 정@@NAMATH_INLINE@@n@@NAMATH_INLINE@@각형의 넓이는 삼각형 @@NAMATH_INLINE@@\text{OAC}@@NAMATH_INLINE@@의 넓이의 @@NAMATH_INLINE@@n@@NAMATH_INLINE@@배이다. 따라서 원에 내접하는 정@@NAMATH_INLINE@@n@@NAMATH_INLINE@@각형의 넓이 @@NAMATH_DISPLAY@@\text{A}(n)=n\cdot \frac{1}{2} \sin 2\theta=n\cos \theta \sin \theta@@NAMATH_DISPLAY@@이다.

확대보기

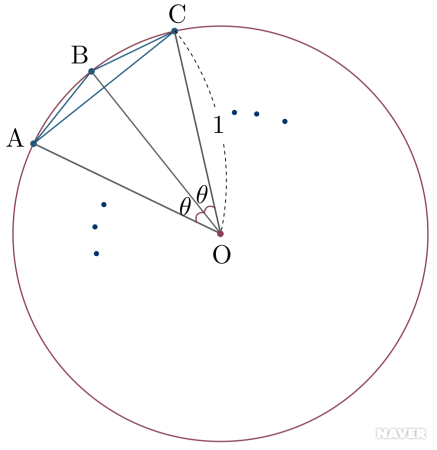
마찬가지 이유로 원에 내접하는 정 @@NAMATH_INLINE@@2n@@NAMATH_INLINE@@각형의 넓이는 @@NAMATH_DISPLAY@@\text{A}(2n)=n \sin \theta@@NAMATH_DISPLAY@@이다. 따라서 @@NAMATH_DISPLAY@@\frac{\text{A}(n)}{\text{A}(2n)}=\cos \theta@@NAMATH_DISPLAY@@이다. 이를 반복 적용하면 임의의 양의 정수 @@NAMATH_INLINE@@k@@NAMATH_INLINE@@에 대하여 @@NAMATH_DISPLAY@@\begin{align} \frac{\text{A}(n)}{\text{A}(2^kn)} &=\frac{\text{A}(n)}{\text{A}(2n)}\times \frac{\text{A}(2n)}{\text{A}(2^2n)}\times \cdots \times \frac{\text{A}(2^{k-1}n)}{\text{A}(2^k n)} \\ &=\cos \theta\cos \left( \frac{\theta}{2} \right) \cdots \cos \left( \frac{\theta}{2^k} \right) \end{align}@@NAMATH_DISPLAY@@이다. 이때 @@NAMATH_INLINE@@k@@NAMATH_INLINE@@를 무한대로 보내면, @@NAMATH_INLINE@@\text{A}(2^k n)@@NAMATH_INLINE@@은 반지름의 길이가 @@NAMATH_INLINE@@1@@NAMATH_INLINE@@인 원의 넓이에 수렴하므로 다음이 성립한다. @@NAMATH_DISPLAY@@\lim_{k \to \infty} \text{A}(2^kn)=\pi @@NAMATH_DISPLAY@@따라서 @@NAMATH_DISPLAY@@\pi=\frac{n \cos \theta \sin \theta}{\cos \theta \cos (\frac{\theta}{2})\cos (\frac{\theta}{2^2}) \cos (\frac{\theta}{2^3}) \cdots }@@NAMATH_DISPLAY@@이다. @@NAMATH_INLINE@@n=4@@NAMATH_INLINE@@라고 하면, @@NAMATH_INLINE@@\theta=45^{\circ}@@NAMATH_INLINE@@가 되어 @@NAMATH_INLINE@@\cos \theta=\sin \theta =\frac{1}{\sqrt{2}}@@NAMATH_INLINE@@이다. 코사인 반각 공식과 이를 이용하면, @@NAMATH_DISPLAY@@\pi= \frac{2}{\sqrt{\frac{1}{2}}\times \sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}}}\times \cdots}@@NAMATH_DISPLAY@@로 표현할 수 있다. 이는 르네상스 시대의 수학자 비에트(Viete)의 아이디어로 @@NAMATH_INLINE@@\pi@@NAMATH_INLINE@@를 무한곱으로 표현한 것이다.

17세기 스코틀랜드 수학자인 제임스 그레고리가 발견한 그레고리 급수 @@NAMATH_DISPLAY@@\text{arctan} x=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdots @@NAMATH_DISPLAY@@를 이용하여 라이프니츠가 @@NAMATH_INLINE@@\pi@@NAMATH_INLINE@@를 다음과 같이 무한급수로 나타내었다. @@NAMATH_DISPLAY@@\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots @@NAMATH_DISPLAY@@ 이 무한급수는 @@NAMATH_INLINE@@\pi@@NAMATH_INLINE@@의 근삿값을 계산하는 좋은 도구이다. 특히 1940년대 말 컴퓨터를 이용한 @@NAMATH_INLINE@@\pi@@NAMATH_INLINE@@의 근삿값 계산에 이 급수가 사용되었다. 마찬가지로 아크사인함수를 이용하면 @@NAMATH_INLINE@@\pi@@NAMATH_INLINE@@의 또 다른 급수 표현을 얻을 수 있는데, 아크탄젠트함수를 이용하여 얻은 급수보다 @@NAMATH_INLINE@@\pi@@NAMATH_INLINE@@로 훨씬 빠르게 수렴한다.

18세기 람베르트(Lambert)가 @@NAMATH_INLINE@@\pi@@NAMATH_INLINE@@가 무리수임을 증명한 이후로 여러 수학자들이 다양한 방법으로 @@NAMATH_INLINE@@\pi@@NAMATH_INLINE@@가 무리수임을 증명하였다. 그런데 @@NAMATH_INLINE@@\pi@@NAMATH_INLINE@@는 무리수일 뿐만 아니라 유리수 계수 방정식의 해가 될 수 없는 수인 초월수이다. 이는 @@NAMATH_INLINE@@\pi@@NAMATH_INLINE@@가 유리수와 유리수의 거듭제곱근꼴의 유한번 결합으로 표시되지 않음을 의미한다. 그러므로 자와 컴퍼스만으로는 @@NAMATH_INLINE@@\pi@@NAMATH_INLINE@@를 작도할 수 없다. 이로부터 주어진 원과 넓이가 같은 정사각형을 자와 컴퍼스만으로는 작도할 수 없음을 알 수 있다.

그레고리 급수, 반지름, 지름, 원주, 파이 (칸아카데미)