수치로 된 자료 중 약 @@NAMATH_INLINE@@100\times p\%@@NAMATH_INLINE@@가 @@NAMATH_INLINE@@a@@NAMATH_INLINE@@보다 작고 약 @@NAMATH_INLINE@@100\times (1-p)\%@@NAMATH_INLINE@@가 @@NAMATH_INLINE@@a@@NAMATH_INLINE@@보다 클 때 '@@NAMATH_INLINE@@a@@NAMATH_INLINE@@의 백분위는 @@NAMATH_INLINE@@100 \times p\,@@NAMATH_INLINE@@이다.'라 하고, @@NAMATH_INLINE@@a@@NAMATH_INLINE@@를 그 자료의 @@NAMATH_INLINE@@100\times p\,@@NAMATH_INLINE@@백분위수 @@NAMATH_INLINE@@(0 \le p \le 1)@@NAMATH_INLINE@@ 라고 한다.
자료에 대하여 백분위수를 정의하는 방법은 여러 가지가 있는데, 정의하는 방법에 따라 백분위수가 다르게 계산된다.
또, 어떤 확률변수 @@NAMATH_INLINE@@X@@NAMATH_INLINE@@에 대하여 @@NAMATH_INLINE@@\text{P}(X \le a) \ge p@@NAMATH_INLINE@@이고 @@NAMATH_INLINE@@\text{P}(X<a) \le p@@NAMATH_INLINE@@를 만족하는 @@NAMATH_INLINE@@a@@NAMATH_INLINE@@를 (@@NAMATH_INLINE@@X@@NAMATH_INLINE@@가 따르는) 그 분포의 @@NAMATH_INLINE@@100\times p\,@@NAMATH_INLINE@@백분위수라 하고 '@@NAMATH_INLINE@@a@@NAMATH_INLINE@@의 백분위는 @@NAMATH_INLINE@@100 \times p\,@@NAMATH_INLINE@@이다.'라고 한다.
자료에 대한 백분위와 백분위수
백분위를 0보다 크고 100보다 작게 정의하는 방법
(정의1)
크기 순으로 나열된 @@NAMATH_INLINE@@K@@NAMATH_INLINE@@개의 자료들이 있을 때, @@NAMATH_INLINE@@n(< K)@@NAMATH_INLINE@@ 번째로 작은 자료의 백분위를 @@NAMATH_INLINE@@100\times p = 100 \times \frac{n}{K+1}@@NAMATH_INLINE@@으로 정하고 그 자료를 @@NAMATH_INLINE@@100\times p\,@@NAMATH_INLINE@@백분위수로 정한다.
@@NAMATH_INLINE@@p \ne \frac{n}{K+1}@@NAMATH_INLINE@@인 @@NAMATH_INLINE@@p@@NAMATH_INLINE@@에 대하여 @@NAMATH_INLINE@@100\times p\,@@NAMATH_INLINE@@백분위수는 선형보간법(linear interpolation)을 적용한다.
@@NAMATH_INLINE@@p<\frac{1}{K+1}@@NAMATH_INLINE@@ 이거나 @@NAMATH_INLINE@@p>\frac{K}{K+1}@@NAMATH_INLINE@@ 인 @@NAMATH_INLINE@@p@@NAMATH_INLINE@@에 대하여 @@NAMATH_INLINE@@100 \times p\,@@NAMATH_INLINE@@백분위수는 정의하지 않는다.
보기1
다음과 같이 최솟값이 215이고 최댓값이 297인 자료가 있다고 하자. 자료의 개수는 9이다.
각 자료에 대하여 백분위를 @@NAMATH_INLINE@@100 \times p@@NAMATH_INLINE@@로 부여할 때, 해당하는 @@NAMATH_INLINE@@p@@NAMATH_INLINE@@를 표에 정리하였다.
| 자료 | 215 | 225 | 250 | 260 | 265 | 280 | 290 | 295 | 297 |
| p | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
이때 자료 225의 백분위는 20, 자료 265의 백분위는 50이다. 다시 말해 자료의 20백분위수 = 225이고 자료의 50백분위수 = 265 이다.
그리고 가장 작은 자료인 215의 백분위는 10이고 가장 큰 자료인 297의 백분위는 90이다.
@@NAMATH_INLINE@@p \ne \frac{n}{10}@@NAMATH_INLINE@@일 때, @@NAMATH_INLINE@@100\times p\,@@NAMATH_INLINE@@백분위수는 선형보간법을 적용한다.
예로서, 70백분위수가 290이고 80백분위수가 295이므로 @@NAMATH_DISPLAY@@\text{75백분위수} = \frac{\text{70백분위수}+\text{80백분위수}}{2} = \frac{290+295}{2}= 292.5 @@NAMATH_DISPLAY@@이고 @@NAMATH_DISPLAY@@\text{28백분위수} = \frac{2}{10} \times \text{20백분위수}+ \frac{8}{10} \times \text{30백분위수} = \frac{2}{10} \times 225 + \frac{8}{10} \times 250 = 245 @@NAMATH_DISPLAY@@이다. 그리고 4백분위수, 91백분위수 등은 정의하지 않는다.
50백분위수와 중앙값(1)
(정의1)에 의한 50백분위수의 정의와 전통적인 중앙값의 정의가 일치한다.
참고로 중앙값의 정의는 다음과 같다.
자료의 개수가 홀수(@@NAMATH_INLINE@@= 2k-1@@NAMATH_INLINE@@)개일 때, @@NAMATH_DISPLAY@@\text{중앙값} = k\text{번째로 작은 자료} @@NAMATH_DISPLAY@@이다. 예를 들어, 99개의 자료에서는 순서상 가운데 있는 50번째 자료가 중앙값이다.
자료의 개수가 짝수(@@NAMATH_INLINE@@=2k@@NAMATH_INLINE@@)개일 때, @@NAMATH_DISPLAY@@\text{중앙값} = \frac{k\text{번째로 작은 자료} + (k+1)\text{번째로 작은 자료}}{2} @@NAMATH_DISPLAY@@이다. 예를 들어, 100개의 자료에서는 순서상 가운데 있는 두 자료(50번째 자료와 51번째 자료)의 산술평균이 중앙값이다.
백분위를 0 이상 100 이하로 정의하는 방법
(정의2)
크기 순으로 나열된 @@NAMATH_INLINE@@K@@NAMATH_INLINE@@개의 자료들이 있을 때, @@NAMATH_INLINE@@n(<K)@@NAMATH_INLINE@@번째로 작은 자료의 백분위를 @@NAMATH_INLINE@@100 \times p = 100 \times \frac{n-1}{K-1}@@NAMATH_INLINE@@로 정하고 그 자료를 @@NAMATH_INLINE@@100\times p\,@@NAMATH_INLINE@@백분위수로 정한다.
@@NAMATH_INLINE@@p \ne \frac{n-1}{K-1}@@NAMATH_INLINE@@인 @@NAMATH_INLINE@@p@@NAMATH_INLINE@@에 대하여 @@NAMATH_INLINE@@100\times p\,@@NAMATH_INLINE@@백분위수는 선형보간법(linear interpolation)을 적용한다.
(정의2)에 따르면 자료 중 최솟값의 백분위는 0이고 최댓값의 백분위는 100이다.
보기2
다음과 같이 최솟값이 305이고 최댓값이 395인 자료가 있다고 하자. 자료의 개수는 6이다.
각 자료에 대하여 백분위를 @@NAMATH_INLINE@@100 \times p@@NAMATH_INLINE@@로 부여할 때, 해당하는 @@NAMATH_INLINE@@p@@NAMATH_INLINE@@를 표에 정리하였다.
| 자료 | 305 | 310 | 325 | 355 | 365 | 395 |
| p | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
이때 자료 325의 백분위는 40, 자료 365의 백분위는 80이다. 다시 말해 자료의 40백분위수 = 325이고 자료의 80백분위수 = 365 이다.
그리고 가장 작은 자료인 305의 백분위는 0이고 가장 큰 자료인 395의 백분위는 100이다.
@@NAMATH_INLINE@@p \ne \frac{n-1}{5}@@NAMATH_INLINE@@일 때, @@NAMATH_INLINE@@100\times p\,@@NAMATH_INLINE@@백분위수는 선형보간법을 적용한다.
예를 들어, @@NAMATH_DISPLAY@@\text{75백분위수} = \frac{5}{20} \times \text{60백분위수}+ \frac{15}{20} \times \text{80백분위수} = \frac{5}{20} \times 355 + \frac{15}{20} \times 365 = 362.5 @@NAMATH_DISPLAY@@이고 @@NAMATH_DISPLAY@@\text{50백분위수} = \frac{10}{20} \times \text{40백분위수}+ \frac{10}{20} \times \text{60백분위수} = \frac{325+355}{20} = 340 @@NAMATH_DISPLAY@@이다.
50백분위수와 중앙값(2)
(정의2)에 의한 50백분위수의 정의와 전통적인 중앙값의 정의가 일치한다.
확률분포에 대한 백분위와 백분위수
정의
분포함수 @@NAMATH_INLINE@@F(x)@@NAMATH_INLINE@@를 갖는 확률변수 @@NAMATH_INLINE@@X@@NAMATH_INLINE@@에 대하여 @@NAMATH_DISPLAY@@\text{P}(X<a) \le p, \quad \text{P}(X \le a) \ge p @@NAMATH_DISPLAY@@를 만족하는 @@NAMATH_INLINE@@a@@NAMATH_INLINE@@를 이 분포의 @@NAMATH_INLINE@@100 \times p\,@@NAMATH_INLINE@@백분위수라 하고 '@@NAMATH_INLINE@@a@@NAMATH_INLINE@@의 백분위는 @@NAMATH_INLINE@@100 \times p@@NAMATH_INLINE@@'라고 한다. 이 조건은 다음과 같이 바꾸어 쓸 수 있다. @@NAMATH_DISPLAY@@F(a-) \le p, \quad F(a) \ge p @@NAMATH_DISPLAY@@
연속확률분포의 백분위수
연속확률변수 @@NAMATH_INLINE@@X@@NAMATH_INLINE@@의 분포함수가 @@NAMATH_INLINE@@F(x)@@NAMATH_INLINE@@일 때, @@NAMATH_INLINE@@0<p<1@@NAMATH_INLINE@@인 @@NAMATH_INLINE@@p@@NAMATH_INLINE@@에 대하여 @@NAMATH_DISPLAY@@F(a)=p @@NAMATH_DISPLAY@@인 @@NAMATH_INLINE@@a@@NAMATH_INLINE@@가 이 분포의 @@NAMATH_INLINE@@100 \times p\,@@NAMATH_INLINE@@백분위수이다.
연속함수 @@NAMATH_INLINE@@F(x)@@NAMATH_INLINE@@가 순증가함수이면 각 @@NAMATH_INLINE@@p \, (0<p<1)@@NAMATH_INLINE@@에 대하여 @@NAMATH_INLINE@@100 \times p\,@@NAMATH_INLINE@@백분위수는 유일하고, @@NAMATH_INLINE@@p@@NAMATH_INLINE@@에 대하여 @@NAMATH_INLINE@@100 \times p\,@@NAMATH_INLINE@@백분위수를 대응시키는 함수인 @@NAMATH_INLINE@@F^{-1}(p)@@NAMATH_INLINE@@는 이 분포의 분위수 함수와 동일하다.
일반적인 분포의 백분위수
분포함수 @@NAMATH_INLINE@@F(x)@@NAMATH_INLINE@@가 다음과 같다고 하자.
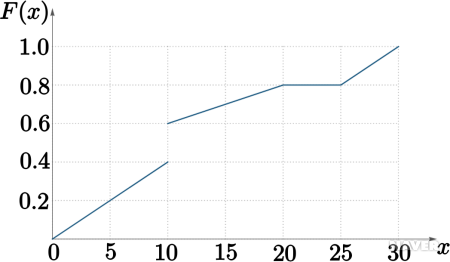
@@NAMATH_INLINE@@F(5-)=0.2@@NAMATH_INLINE@@이고 @@NAMATH_INLINE@@F(5)=0.2@@NAMATH_INLINE@@이므로 @@NAMATH_INLINE@@F@@NAMATH_INLINE@@의 20백분위수는 5이다.
@@NAMATH_INLINE@@F(10-)=0.4@@NAMATH_INLINE@@이고 @@NAMATH_INLINE@@F(10)=0.6@@NAMATH_INLINE@@이므로 @@NAMATH_INLINE@@F@@NAMATH_INLINE@@의 40백분위수, 50백분위수, 60백분위수 모두 10이다.
@@NAMATH_INLINE@@20 \le a \le 25@@NAMATH_INLINE@@인 모든 @@NAMATH_INLINE@@a@@NAMATH_INLINE@@에 대하여 @@NAMATH_INLINE@@F(a-)=F(a)=0.8@@NAMATH_INLINE@@이므로 20 이상 25 이하의 모든 수가 @@NAMATH_INLINE@@F@@NAMATH_INLINE@@의 80백분위수이다.
출처
본 컨텐츠의 저작권은 저자 또는 제공처에 있으며, 이를 무단 이용하는 경우 저작권법 등에 따라 법적책임을 질 수 있습니다.
외부 저작권자가 제공한 콘텐츠는 네이버의 입장과 다를 수 있습니다.
-
제공처
1946년에 설립된 대한수학회는 수학자들의 연구 및 교육 활동이 보다 원활하게 이루어지고 더 나은 환경을 구축하기 위해 지원하며, 수학공동체의 권익 증진과 학술적 가치를 기반으로 국내외 공익 기여를 통한 사회적 책무 수행을 위해 활동하고 있다. 또한 수학문화 확산 및 과학의 여러 부문과 협력하여 학술 문화 발전에 기여해 오고 있다.
매년 봄,가을 정기 연구발표회를 개최하며, 국내 수학 전문 학술지 중 유일하게 SCIE에 등재된 ‘대한수학회지(Journal of the KMS)’와 ‘대한수학회보(Bulletin of the KMS)’, 그리고 ESCI 등재지인 ‘대한수학회논문집(Communications of the KMS)’을 발행하고 있다.